通过量子力学分析氦气原子的组成
世源气体 www.51qiti.com 更新时间：2011-1-5 21:48:00
氦气原子的原子序数Z=2，原子核带2份正电荷，核外有二个电子。二个电子组成全同二体系统。氦气原子的光谱存在二套光谱线系，可推断存在二套能级各自发生量子跃迁，由此历史上曾误认为存在二种氦气原子，正氦气气和仲氦气。通过量子力学对氦气原子问题的求解，揭开了其中的奥秘，原来是自旋在其中扮演了重要角色。
忽略与自旋有关的能量，氦气原子的哈密顿量
%7D%2B%7B%5Cfrac%7B%7B%7B%7Be%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7Br%7D_%7B%7B%7B12%7D%7D%7D%7D%7D%7D%3D%7B%5Chat%7B%7B%7BH%7D%7D%7D%7D_%7B%7B0%7D%7D%2B%7B%5Cfrac%7B%7B%7B%7Be%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7Br%7D_%7B%7B%7B12%7D%7D%7D%7D%7D%7D "hat{H}=sum_{\alpha=1}^2(\frac{1}{2\mu}hat{p}_\alpha^2-\frac{2e^2}{r_\alpha})+\frac{e^2}{r_{12}}=hat{H}_0+\frac{e^2}{r_{12}}")
其中rα=|xα|，r12=|x1-x2|
先求二个独立电子系统哈密顿量
的本征值问题。不计与自旋有关的能量，轨道运动和自旋运动是分离变量的。每个独立单电子的轨道波函数都是Z=2的类氢离子的波函数ψnlm，相应的能量为
。的基态能量为2ε1，低激发态能量为ε1+εn（n≠1）。全同二体系的波函数，对于粒子交换是反对称的，考虑自旋变量，的基态和低激发态的波函数为：
%7D%7D%7D%7D%3D%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D%5Cright)%7D%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cchi_%7B%7B%7B00%7D%7D%7D%5C%5C%7B%5Cpsi_%7B%7B%7B1%7D%7Bn%7D%7Bs%7D%7Bm%7D_%7B%7Bs%7D%7D%7D%7D%5E%7B%7B%7B%5Cleft(%7B0%7D%5Cright)%7D%7D%7D%7D%3D%7B%5Cfrac%7B%7B%7B1%7D%7D%7D%7B%7B%5Csqrt%7B%7B%7B2%7D%7D%7D%7D%7D%7D%7B%5Cleft%5B%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D%5Cright)%7D%5Cpsi_%7B%7B%7Bn%7D%7Bl%7D%7Bm%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cpm%5Cpsi_%7B%7B%7Bn%7D%7Bl%7D%7Bm%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D%5Cright)%7D%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cright%5D%7D%7B%5Cleft.%5Cmatrix%7B%5Cchi_%7B%7B%7B00%7D%7D%7D%5C%5C%5Cchi_%7B%7B%7B1%7D%7Bm%7D_%7B%7Bs%7D%7D%7D%7D%7D%5Cright.%7D%7D%5Cright%5Crbrace%7D "{:[\psi_g^{(0)}=\psi_{100}(bb{x}_1)\psi_{100}(bb{x}_2)\chi_{00}],[\psi_{1nsm_s}^{(0)}=\frac{1}{sqrt{2}}[\psi_{100}(bb{x}_1)\psi_{nlm}(bb{x}_2)\pm\psi_{nlm}(bb{x}_1)\psi_{100}(bb{x}_2)]{:[\chi_{00}],[\chi_{1m_s}]:}]}")
（1）
其中χsms是二个电子自旋合成的耦合基；χ00是自旋单态；χ1ms是自旋三重态，ms=1,0,-1；它们的表达式如下
%7D%5Cxi_%7B%7B-%7D%7D%7B%5Cleft(%7B2%7D%5Cright)%7D-%5Cxi_%7B%7B-%7D%7D%7B%5Cleft(%7B1%7D%5Cright)%7D%5Cxi_%7B%7B%2B%7D%7D%7B%5Cleft(%7B2%7D%5Cright)%7D%5Cright%5D%7D "\chi_{00}=\frac{1}{sqrt{2}}[\xi_{+}(1)\xi_{-}(2)-\xi_{-}(1)\xi_{+}(2)]")
χ11=ξ+(1)ξ+(2)
%7D%5Cxi_%7B%7B-%7D%7D%7B%5Cleft(%7B2%7D%5Cright)%7D%2B%5Cxi_%7B%7B-%7D%7D%7B%5Cleft(%7B1%7D%5Cright)%7D%5Cxi_%7B%7B%2B%7D%7D%7B%5Cleft(%7B2%7D%5Cright)%7D%5Cright%5D%7D "\chi_{10}=\frac{1}{sqrt{2}}[\xi_{+}(1)\xi_{-}(2)+\xi_{-}(1)\xi_{+}(2)]")
χ1,-1=ξ-(1)ξ-(2)
其中ξ±代表自旋朝上、下的自旋态。式（1）已满足粒子交换反对称要求，等价于计入了全同粒子的量子相互作用能量。在此基础上，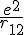
可作微扰处理。由微扰论求得能量：
⑴基态
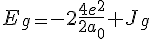
%7D%5Cright%7C%7D%7D%5E%7B%7B2%7D%7D%7B%7B%5Cleft%7C%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cright%7C%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7B%5Cleft%7C%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D-%7B%5Cmathbf%7B%7B%7Bx%7D_%7B%7B2%7D%7D%7D%7D%7D%5Cright%7C%7D%7D%7D%7D "J_g=e^2intint d^3x_1d^3x_2\frac{|\psi_{100}(bb{x}_1)|^2|\psi_{100}(bb{x}_2)|^2}{|bb{x}_1-bb{x_2}|}")
数值计算结果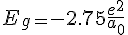
，和实验值
基本一致。采用变分法计算，理论值和实验值符合得很好；
⑵低激发态
%7D%2B%7BJ%7D%5Cpm%7BK%7D "E_{nl}=\frac{-4e^2}{2a_0}(1+\frac{1}{n^2})+J\pmK")
（2）
%7D%5Cright%7C%7D%7D%5E%7B%7B2%7D%7D%7B%7B%5Cleft%7C%5Cpsi_%7B%7B%7Bn%7D%7Bl%7D%7Bm%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cright%7C%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7B%5Cleft%7C%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D-%7B%5Cmathbf%7B%7B%7Bx%7D_%7B%7B2%7D%7D%7D%7D%7D%5Cright%7C%7D%7D%7D%7D "J=e^2intint d^3x_1d^3x_2\frac{|\psi_{100}(bb{x}_1)|^2|\psi_{nlm}(bb{x}_2)|^2}{|bb{x}_1-bb{x_2}|}")
%7D%5Cpsi_%7B%7B%7Bn%7D%7Bl%7D%7Bm%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D%5Cright)%7D%7B%5Cpsi_%7B%7B%7Bn%7D%7Bl%7D%7Bm%7D%7D%7D%5E%7B%5Cast%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%5Cpsi_%7B%7B%7B100%7D%7D%7D%7B%5Cleft(%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B2%7D%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft%7C%7B%5Cmathbf%7B%7B%7Bx%7D%7D%7D%7D_%7B%7B1%7D%7D-%7B%5Cmathbf%7B%7B%7Bx%7D_%7B%7B2%7D%7D%7D%7D%7D%5Cright%7C%7D%7D%7D%7D "K=e^2intint d^3x_1d^3x_2\frac{\psi_{100}^\**(bb{x}_1)\psi_{nlm}(bb{x}_1)\psi_{nlm}^\**(bb{x}_2)\psi_{100}(bb{x}_2)}{|bb{x}_1-bb{x_2}|}")
其J、K分别称为平均库仑能和交换能，它们的值均大于零且和角量子数l有关。对于自旋单态χ00，式（1）的轨道运动波函数是对称的，式（2）中取+K；对于自旋三重态χ1ms，式（1）的轨道运动波函数是反对称的，式（2）中取-K。对于粒子的靠近x1=x2，轨道对称波函数表明其概率比波函数未对称化时ψ100(x1)ψnlm(x2)的概率增大；轨道反对称波函数表明x1=x2的概率减少到零。这些因素是引起±K修正的原因。波函数的对称性质，等价地反映了全同粒子的量子力学相互作用。对于自旋单态和三重态，±K的不同产生1Enl和3Enl二套能级。对于电子跃迁，自旋磁矩不变，即有选择定则ΔS=0，故两套能级各自跃迁，形成两套氦气光谱线系。如图，正氦气的3S1能级虽比仲氦气的1S0高，但由于受ΔS=0的限制而不发生跃迁，因此3S1能级成为亚稳态能级。
对氦气原子的量子力学求解，虽然忽略了与自旋有关的能量，但由于自旋态的交换对称性质不同，直接影响到轨道态的对称或反对称组合，从而影响电子的概率分布和电子间的相互作用能量，即影响到氦气原子的能量。
忽略与自旋有关的能量，氦气原子的哈密顿量
其中rα=|xα|，r12=|x1-x2|
先求二个独立电子系统哈密顿量
其中χsms是二个电子自旋合成的耦合基；χ00是自旋单态；χ1ms是自旋三重态，ms=1,0,-1；它们的表达式如下
χ11=ξ+(1)ξ+(2)
χ1,-1=ξ-(1)ξ-(2)
其中ξ±代表自旋朝上、下的自旋态。式（1）已满足粒子交换反对称要求，等价于计入了全同粒子的量子相互作用能量。在此基础上，
⑴基态
数值计算结果
⑵低激发态
其J、K分别称为平均库仑能和交换能，它们的值均大于零且和角量子数l有关。对于自旋单态χ00，式（1）的轨道运动波函数是对称的，式（2）中取+K；对于自旋三重态χ1ms，式（1）的轨道运动波函数是反对称的，式（2）中取-K。对于粒子的靠近x1=x2，轨道对称波函数表明其概率比波函数未对称化时ψ100(x1)ψnlm(x2)的概率增大；轨道反对称波函数表明x1=x2的概率减少到零。这些因素是引起±K修正的原因。波函数的对称性质，等价地反映了全同粒子的量子力学相互作用。对于自旋单态和三重态，±K的不同产生1Enl和3Enl二套能级。对于电子跃迁，自旋磁矩不变，即有选择定则ΔS=0，故两套能级各自跃迁，形成两套氦气光谱线系。如图，正氦气的3S1能级虽比仲氦气的1S0高，但由于受ΔS=0的限制而不发生跃迁，因此3S1能级成为亚稳态能级。
对氦气原子的量子力学求解，虽然忽略了与自旋有关的能量，但由于自旋态的交换对称性质不同，直接影响到轨道态的对称或反对称组合，从而影响电子的概率分布和电子间的相互作用能量，即影响到氦气原子的能量。
友情链接:
广州市谱源气体有限公司版权所有2006-2013 粤ICP备08114730号
工厂地址：广东省广州市增城新塘镇西洲大王岗工业区
电话: 4006-377-517,020-82797785,13711176807曾小姐 传真: 020－82797482
电话: 4006-377-517,020-82797785,13711176807曾小姐 传真: 020－82797482
技术支持：沁盟科技
